众所周知,有限元分析中单元设置不当会造成计算的误差,其中最常见的就是剪力锁死和沙漏效应。下面就这剪力自锁和沙漏效应来讨论下有限元仿真分析误差的来源。
一、高斯积分
要搞清楚沙漏效应和剪力自锁,先从单元平衡方程说起。我们知道有限元的单元平衡方程是通过最小势能原理推出来的。最小势能原理长这个样子。
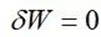
看着好简单,但简单的公式往往蕴含着极深刻的道理。这个公式在说平衡状态的位移场,使得总势能取极值。总势能包括应变能和外力势能,这样公式就变成这样。
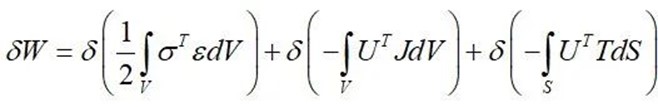
从表达式来看,应变能:
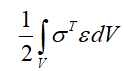
体积力势能:
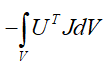
面力势能:
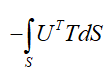
发现这些都需要求积分。对计算机来说,求积分是困难的,但求和就很方便。于是工程师就开始找数学工具,就找到了高斯积分。高斯在几百年前,就发现一个定积分可以近似等于多项式求和,高斯积分公式如下所示。
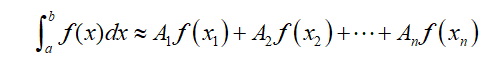
其中:
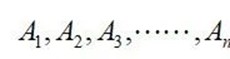
叫做高斯积分权;
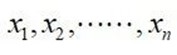
叫高斯积分点。
二、剪力自锁下一个概念完全积分,就是高斯积分点的个数可以对单元的刚度矩阵可以精确积分,其中一次单元每个方向两个,二次单元每个方向三个。示意图如下。
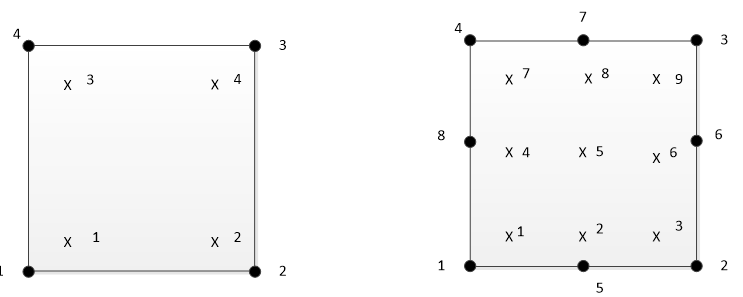
对于受弯载荷单元,单元变形应该如下所示。
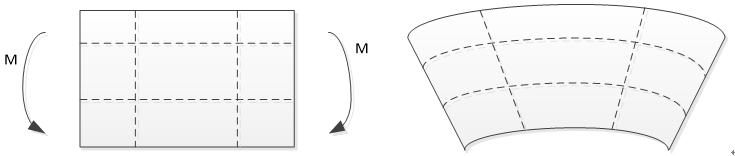
完全积分的一次单元由于一次单元无法模拟弯曲,导致单元的刚度变大,示意图如下。

如图所示,在积分点处水平虚线和竖直虚线的夹角不再为90度,这样剪应变就产生了。可能会导致计算结果不可信。
1、算例演示给出一个悬臂梁例的算例,如下所示。

通过材料力学,我们知道悬臂梁端部的位移为:
利用workbench来仿真,看看剪力自锁到底会带来什么样的误差?workbench中单元属性一般是自动赋予的,大家可能不知道怎么设置单元属性,首先设置完全积分,要在Gemetry中将Element control设置成manual,如下所示。
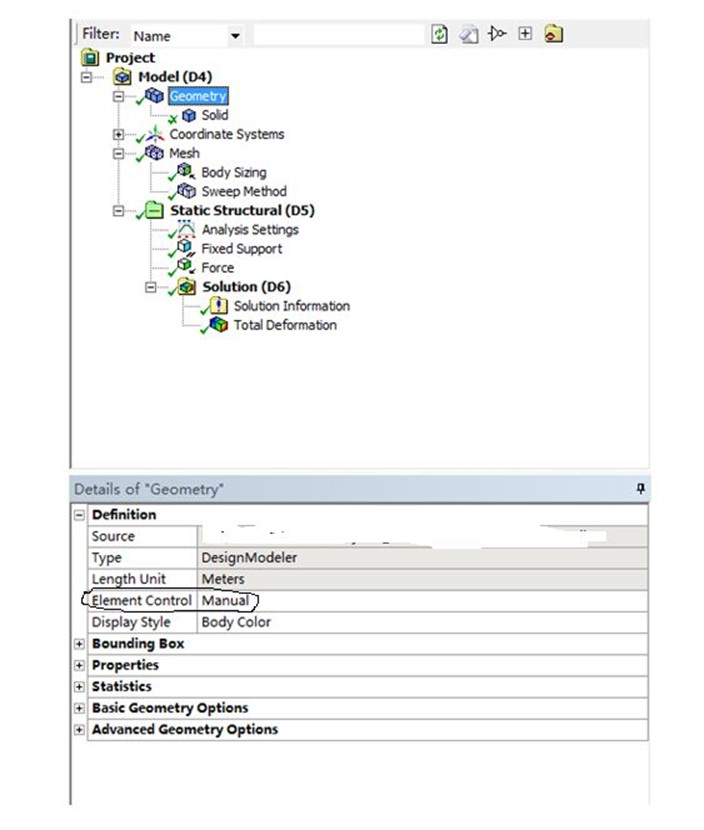
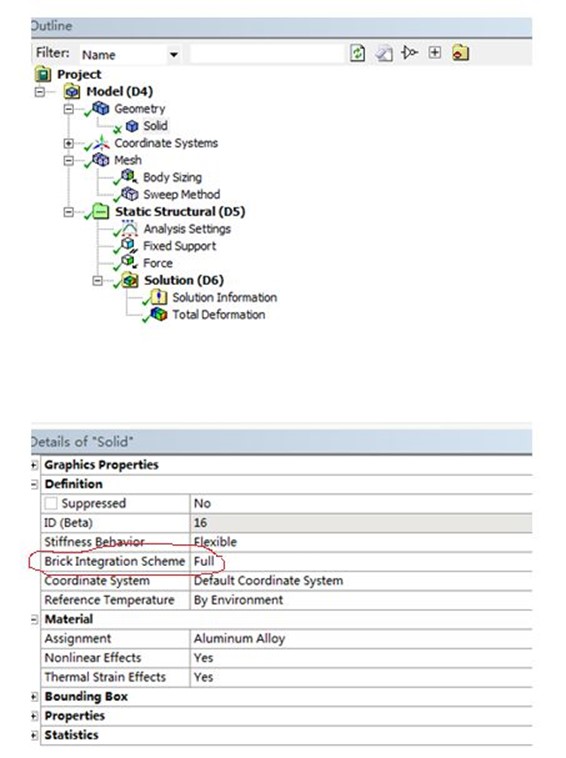
这个时候才可以对模型进行单元属性设置,找到相关模型中Brick Integration scheme设置成Full,如下图所示。
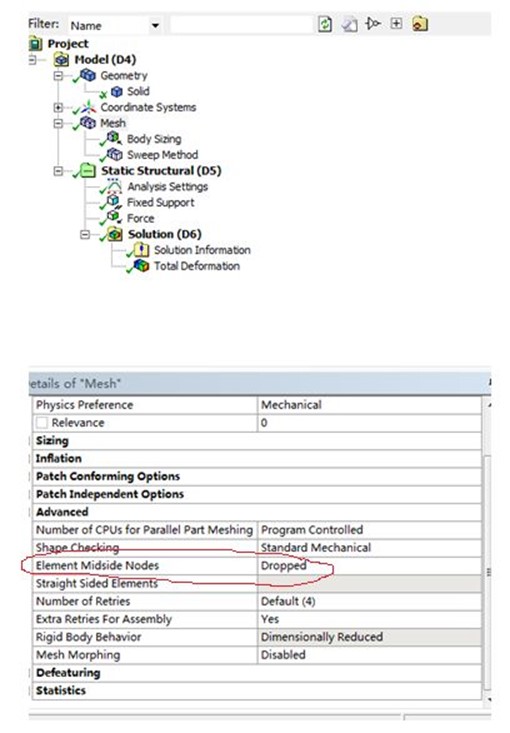
这是对完全积分设置,下面对一次单元进行设置,在mesh中将Element Midside Nodes改成Drop就是一次单元了,如下所示。
计算得到结果如下
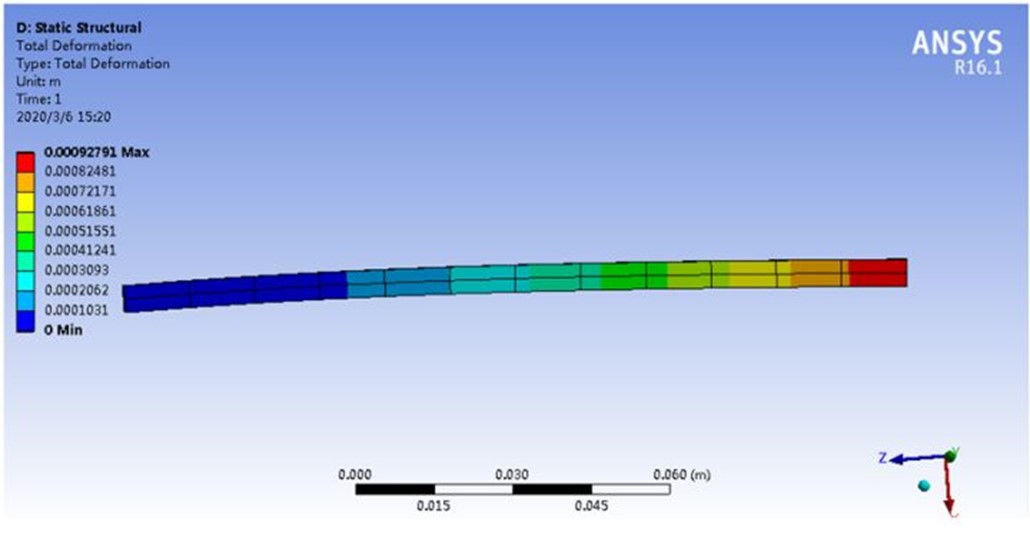
端部位移为0.93mm,误差达到了70%,是不可接受的。在将网格细化后,再计算,结果如下。
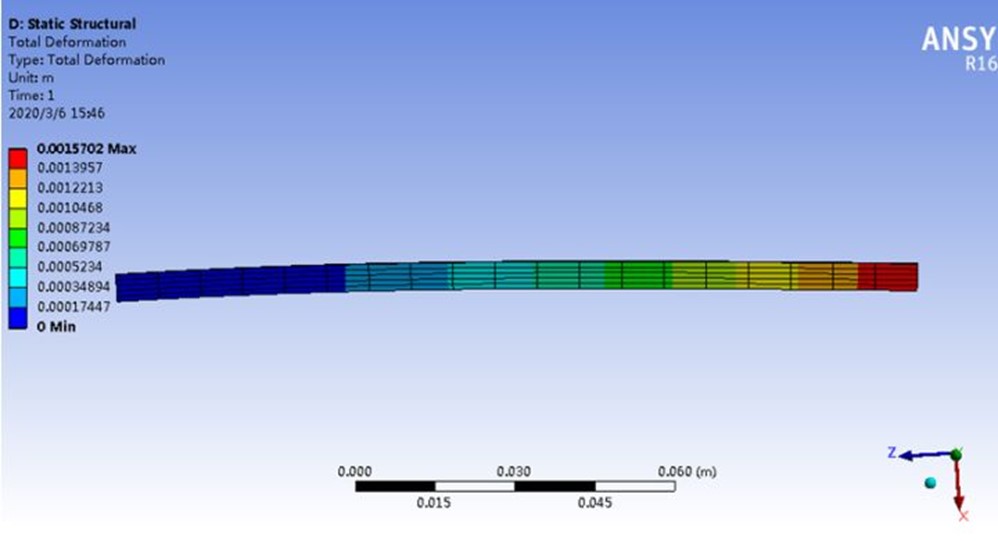
端部位移为0.0015mm,误差为50%。将一次单元变为二次单元,用同样的网格条件,看看计算结果,如下。
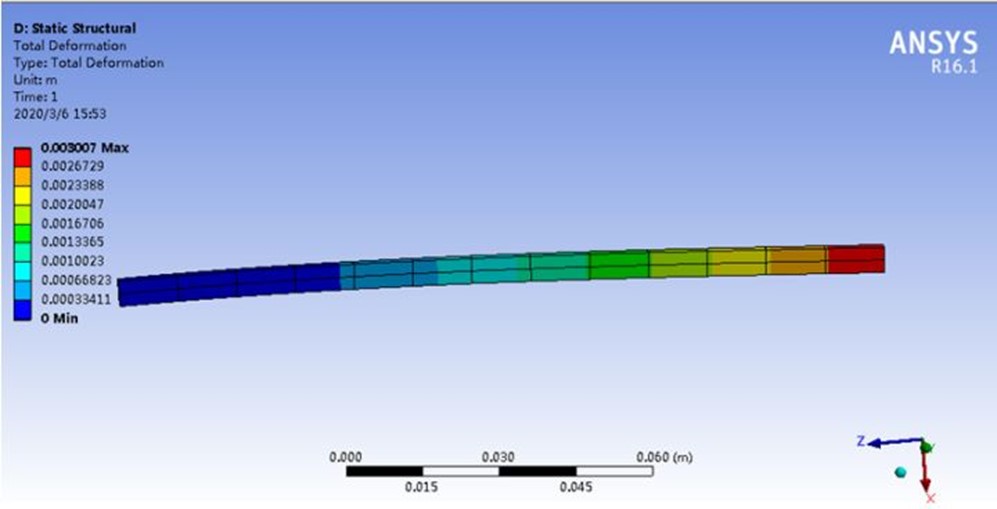
计算结果为3mm,误差3%,可以接受。
将应变在不同的单元提取出来,一次单元的应变情况如下。
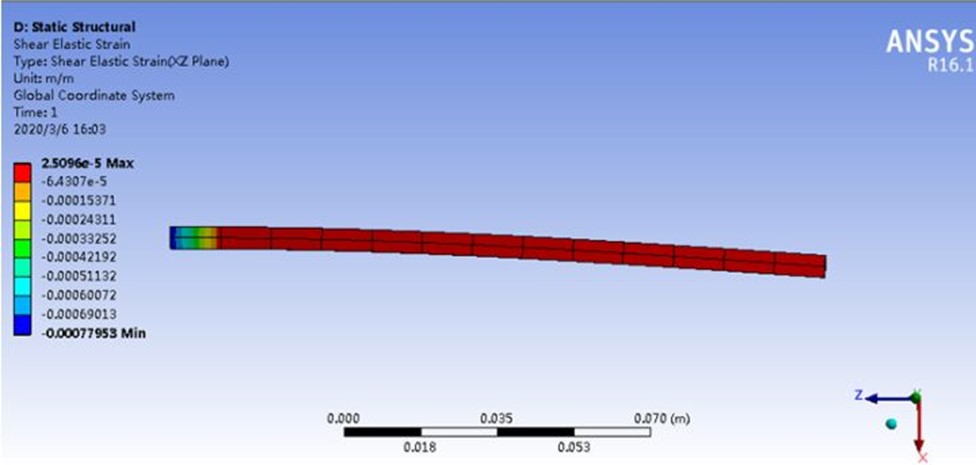
看剪应变的绝对值,即0.0007。二次单元的应变情况如下。
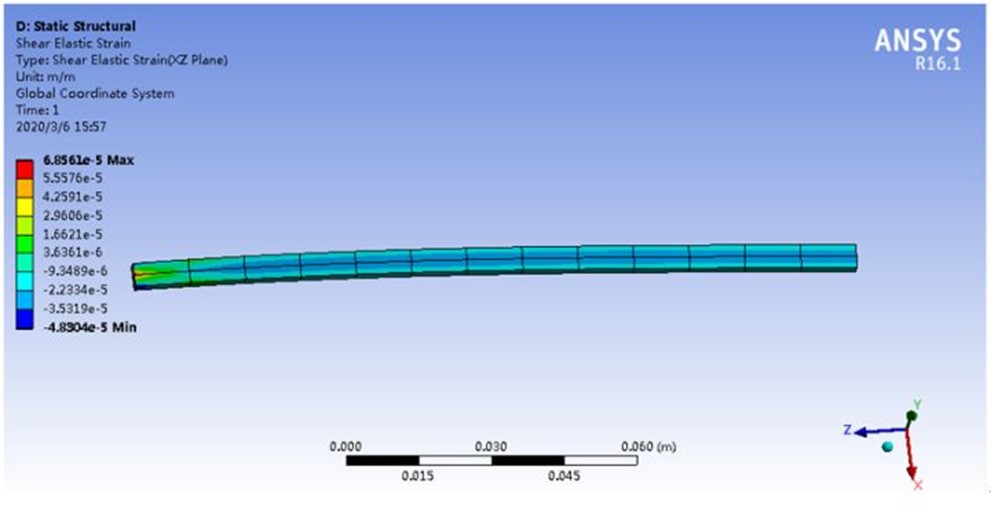
看剪应变的绝对值,即
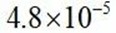
看到在完全积分时,一次单元产生了较大的剪应变,即发生了剪力自锁现象。当然剪力自锁不一定对计算结果产生那么大影响,我们细化网格再计算,结果如下。
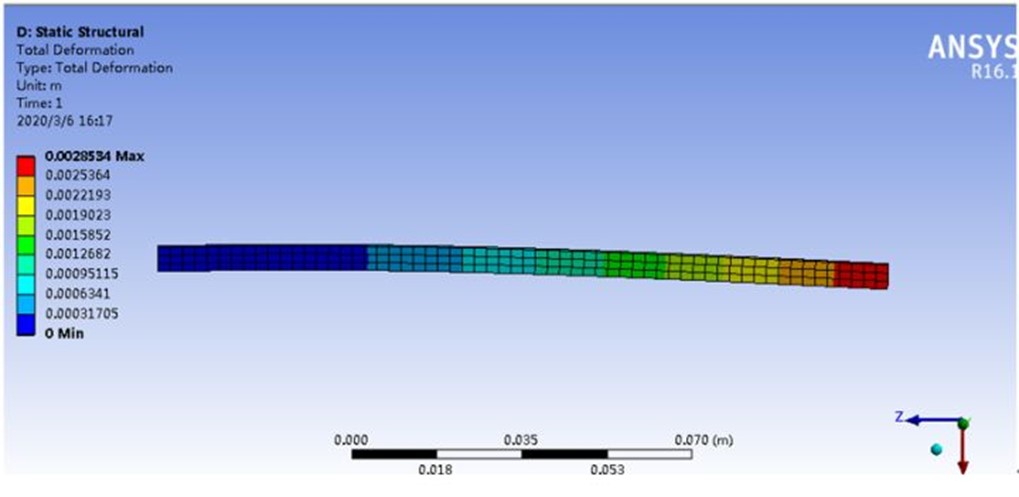
计算结果为2.85mm,误差8%,还是可以接受的。
2、剪力自锁结论
1)受弯曲载荷时,采用完全积分的一次单元,会产生剪力自锁,对计算精度产生影响;采用完全积分的二次单元,则不会产生剪力自锁,计算精度高。
2)网格细化,降低网格长细比,可以提高计算精度,降低剪力自锁带来的影响。
三、沙漏效应
1、模态计算
不知道大家在做模态分析时,会不会遇到这样的情况。
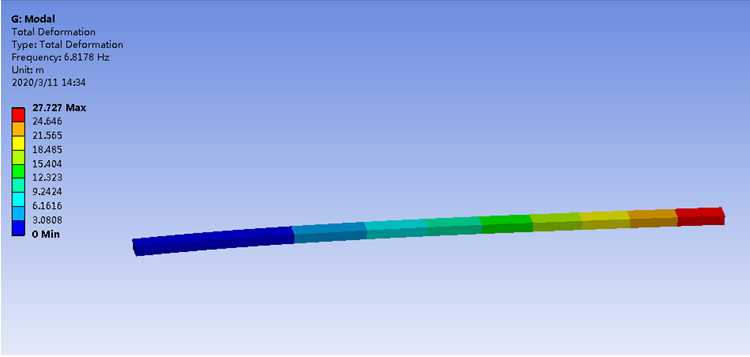
以前文中悬臂梁的例子,从图中可以看出一阶固有频率只有6.8Hz,这个结果可信吗?我们验证下,固有频率的计算公式如下。
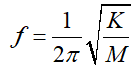
K 是模态刚度, M 是模态质量。
这两个参数好像都不会计算,不着急,先计算刚度。对图中振型进行观察,发现第一阶固有频率是整体表现的起伏。那我们就可以通过挠度来计算,悬臂梁的挠度计算公式,大家没忘吧。
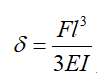
把这个公式变形下,公式如下所示。
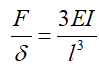
那么模态刚度 :
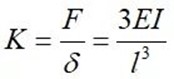
计算得到刚度:
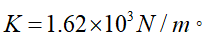
还有质量呢?我们还是观察振型,发现这个振型几乎是整个模型参与的,那么就认为这阶模态质量就是整个模型的质量:
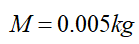
代入公式1中,得到一阶固有频率为 :
这个和仿真的数值差太远,为什么会这样呢?
从单元设置上,我将单元设置为减缩积分的一次单元,会不会跟这个有关呢?
2、减缩积分
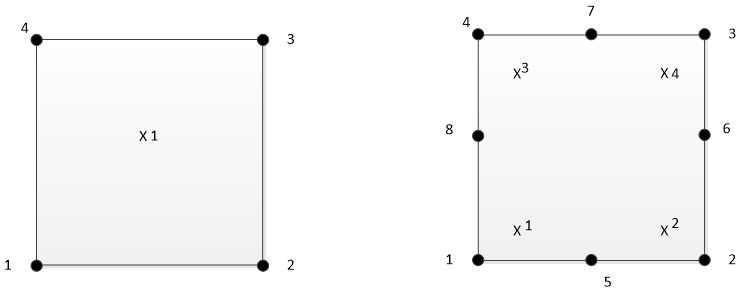
上篇文章中讨论了完全积分,这次说下减缩积分。减缩积分比完全积分在每个方向上少用一个积分点,那么减速积分状态下的一次单元和二次单元积分点的分布,如下所示。
这样当单元受弯时,就会产生这样的情况,如下所示。
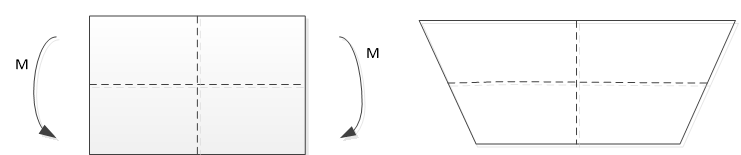
这样中间的横线,实际上既没有伸长,也没有缩短,所以单元没有产生正应力。此外,横线和竖线的夹角也没有发生变化,所以单元也没有产生剪应力。单元什么应力也没有,所以单元不能承受任何载荷,即刚度为零。这就是沙漏效应。
3、案例演示
把一次单元换成二次单元,在计算下模态。
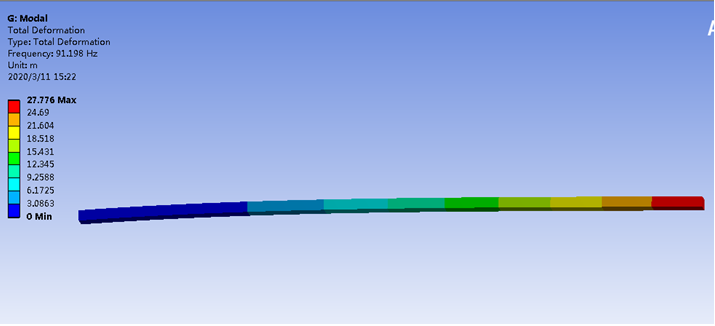
仿真得到结果为91.2Hz。同理论计算值相比,只有0.6%的误差。
减缩积分的二次单元是不是就不存在沙漏现象呢?如果把网格化的粗一些,计算结果变成如图所示。
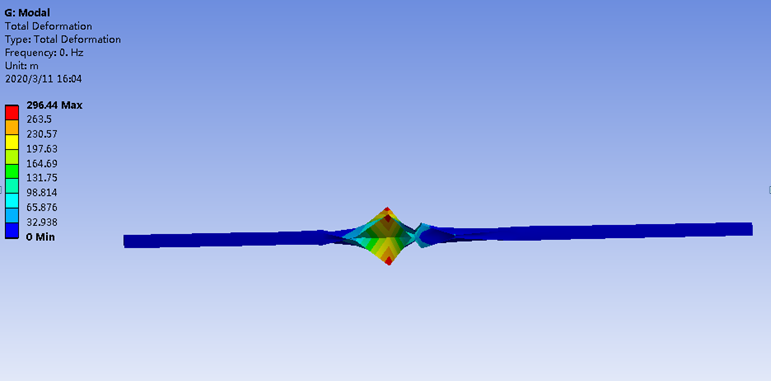
一阶固有频率变成0Hz,不光是一阶固有频率,其他阶的也都变成0或者很小的数值,如下所示。
为什么会这样呢?实际上跟单元的长细比有关,如果单元特别细长,积分点就会非常接近,极限情况两条积分线重合在一起。如下所示。
我们看变形后的单元形状,二次单元可以弯曲,那么竖线和横线的夹角是90度,所以单元没有剪应力。单元特别细长,横线基本位于中性层,那么它也不会伸长或缩短,所以没有正应力。那么沙漏效应又产生了。
-
沙漏效应总结
(1)在减缩积分情况下,不管是一次单元还是二次单元,都有可能产生沙漏效应。要消除沙漏效应,就要提高网格质量,减小网格的长细比。
(2)减缩积分可以有效的排除剪力自锁的影响,不会产生刚度过大的情况。
![]()

