显式动力学是采用显式算法进行动力学方程的求解。显式算法最大优点是有较好的稳定性。不存在隐式算法中的收敛性问题。
显式动力学最适合发生在短时间，几毫秒内的事件或更小时间。持续1秒以上的事件可以模拟但是需要较长的时间，通过诸如质量缩放和动态松弛之类的技术可用于提高模拟效率减少计算时长。
显示动力学的一些主要应用领域为：材料的动态力学响应，汽车的碰撞，高速切削、电子产品的跌落、流固耦合、军事工业中的战斗部的设计等。
动态显式算法采用动力学方程的差分格式，不用直接求解刚度矩阵，不需要进行平衡迭代，计算速度快，时间步长只要取的足够小，一般不存在收敛性问题，因此需要的内存也比隐式算法要少，对于材料的大变形和非线性的求解有较好的模拟。并且数值计算过程可以很容易地进行并行计算，程序编制也相对简单。但显式算法要求质量矩阵为对角矩阵，对网格质量要求较高。而且只有在单元计算尽可能少时速度优势才能发挥, 因而往往采用减缩积分方法，容易激发沙漏模式，影响应力和应变的计算精度。
隐式算法中，在每一增量步内都需要对静态平衡方程进行迭代求解，并且每次迭代都需要求解大型的线性方程组，这个过程需要占用相当数量的计算资源、磁盘空间和内存。该算法中的增量步可以比较大，至少可以比显式算法大得多，但是实际运算中上要受到迭代次数及非线性程度的限制，需要取一个合理值。
使用显式方法，计算成本消耗与单元数量成正比，并且大致与最小单元的尺寸成反比，应用隐式方法，对于许多问题的计算成本大致与自由度数目的平方成正比。
可以这样认为：显式求解器更适合于非线性问题，工作计算量较小，但可以在更高的频率下进行大量的迭代，这些迭代可以跟随物理参数的变化。隐式求解器对每次迭代的计算都要复杂得多，但是它们的数量要少得多。
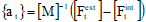
用中心差分法在时间t求加速度：
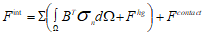
{Ftext}为施加外力和体力矢量。{Ftint}为下式决定的内力矢量。
Fhg为沙漏阻力；Fcont为常量力。
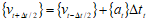
速度与位移用下式得到：
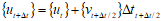
式中
Dtt+Dt/2=.5(Dtt+ Dtt+ Dt) ；
Dtt- Dt/2=.5(Dtt– Dtt+ Dt)
新的几何构形由初始构形加上 {xo}获得:
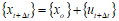
非线性问题：
-
块质量矩阵需要简单转置。
-
方程非耦合，可以直接求解(显式)。
-
无须转置刚度矩阵，所有非线性（包括接触）都包含在内力矢量中。
-
内力计算是主要的计算部分。
-
无须收敛检查。
-
保持稳定状态需要小的时间步。
Author: Taochun Yang
佐雍得尝，与众分享，收获快乐！
